Magic: The Machine Learning

In the previous post on this topic, we raised the question on how much particular abilities such as “flying” cost in the widely known trading card game Magic the Gathering. We found luckily there is a nice, usable free database out there that should be helpful to answer this and while trying to take a look into the data we learned about Prinicipal Component Analysis and how it can be helpful to visualize high-dimensional data.

Somewhat unsatisfactory we ended up without getting an answer to the “flying” question, lets try to come up with a model now that can help with that.

Shouldn’t we just use deep convolutional neural networks or something?

Recently that seems to be the hammer that makes almost everything look like a nail, and I would be lying would I assure you that the recent advances in this area had not motivated this blog post. But, valued reader, keep in mind the question we are trying to answer: How much mana do abilities such as “flying” cost? How much does it cost to have a creature that has one unit more power or toughness? A (deep) neural network might be able to predict accurately the mana cost for any given card, but how would that answer our question? What we are actually after here is not approximating the mana cost of certain cards but understand how they are composed. While neural networks have recently proven to be useful function approximators for various tasks recently, they could not be farther away from something that provides a human-understandable model.

The linear model

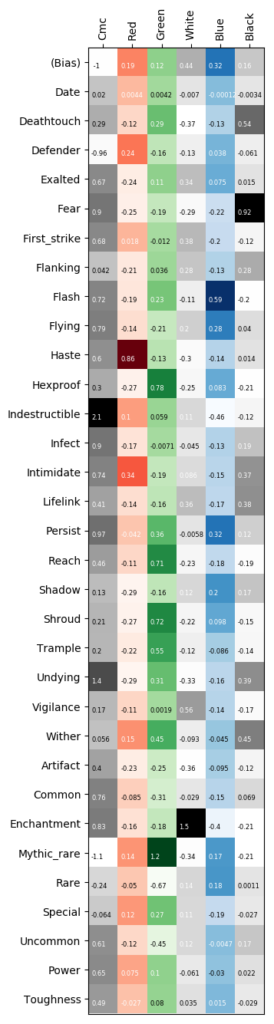
Let’s assume (for now at least), that all cards have the same base cost (bias) of some amount to which the cost for each ability of the card and costs per unit power/toughness are added. That is, we can think of our model as a linear function on our feature vectors that returns a vector of converted mana cost and devotion to each of the five colors.

Let us get straight what we can expect from such a model. There are actually creatures with nonzero strength/toughness out there that have zero mana cost, so the cost bias (that is, the cost of a hypothetical 0/0 creature card without abilities) will probably be negative. Then there are some abilities that are very color-bound which we would expect to show up in the devotion column. E.g. creatures with haste usually require red mana to play out, so we expect some component in the red devotion column for this ability. And last but not least we expect most abilities to cost some (positive) amount of mana, while very few (such as defender) are actually more of a downside and should make the creature cheaper, showing as negative values.

But now without further ado, lets run some regression on this bad boy and see what comes out of it. Scikit’s LinearRegression() finds the parameters you see in the right picture.

Linear model evaluation

According to this model, a hypothetical 0/0 creature card without further abilities would cost -1 mana. There is a yearly inflation of 0.02 CMC mana points on average and power is more costly than toughness. Fear is black, haste is red, hexproof greed, flash blue and vigilance and enchantment creatures are a white concept. So far, the results seem pretty plausible. The impatient reader might also have discovered that the answer to our question on the price of “flying” is 0.79 mana points. So far, so good, but how accurate is our model, anyhow?

According to SciKit-Learn it has a score of s = 0.59… on the training (!) set. That doesn’t sound too god, but what exactly does it mean? The documentation reveals this score value is computed like this:

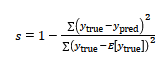
Name	loss	CMC	pred.
Lucent Liminid	0.00	5	5.00
Vorapede	0.00	5	5.00
Hussar Patrol	0.00	4	4.00
Maritime Guard	0.00	2	2.00
Bronze Sable	0.00	2	2.00
…
Shadow Rider	0.38	4	3.62
Alpine Grizzly	0.38	3	3.38
Tor Giant	0.38	4	3.62
Phyrexian Hulk	0.38	6	5.62
…
Caravan Hurda	1.58	5	3.42
Eldrazi Devastator	1.63	8	9.63
Vorstclaw	1.71	6	7.71
Quilled Slagwurm	1.89	7	8.89
Plumeveil	1.91	3	4.91
Zephid	1.95	6	4.05
Merfolk of the Depths	2.01	6	3.99
Phyrexian Walker	2.02	0	2.02
Risen Sanctuary	2.03	7	9.03
Ornithopter	2.37	0	2.37
Kalonian Behemoth	2.43	7	9.43
Fusion Elemental	3.93	5	8.93

In the figure I’ve selected an extract that shows the few best, median and worst regression results. We see that the median error in is 0.38 CMC points which doesn’t seem all too bad, given that we are using a very straightforward model. In the worst case (Fusion Elemental) however this goes up to 3.93! Whats going on here? It turns out there are different causes for the wrong predictions, lets go through them one by one by example.

Fusion Elemental

Fusion Elemental (as many other cards in the game), is quite hard to bring into play. Experienced players will immediately see why: Its not the fact that it has a CMC of 5, it is the fact that this 5 mana has to come from 5 different colors which is harder to achieve than 5 times the same color (I’ll save you and myself digging into the combinatoric possibilities of deck construction).

So why does this cause a bad prediction? Well, in the beginning we assumed that each keyword “costs” a certain (be it fractional) amount in terms of CMC, and maybe in specific colors.

What we totally neglected is that it actually costs “making the card somewhat harder to play”, which can manifest itself in multiple ways. Often through high CMC, but from time to time also through hard-to-play color combinations. To some degree our model seems to compensate for this effect (Hussar Patrol is estimated perfectly), but obviously not for 5-colored cards.

So in fact we need to consider a latent variable which expresses the cards “utility” (usefullness and hardness to bring into play), which can manifest itself in different cost configurations.

Kalonian Behemoth

Our model estimated a 9/9 card with shroud to be worth about 9.43 mana, which (at least to me) doesn’t sound entirely unreasonable. Lets think a second about what “shroud” does: It forbids anyone to play spells on that creature. Usually this is a good thing (our model things its worth 0.21 increase in CMC), as it prevents your opponent from immobilizing your creature (e.g. pacifism) or destroying it (e.g. terror). But it also prevents you from equipping the creature with additional abilities. In this particular example of a creature with very high power value you might likely want to give her an ability like trample. Trample means when your creature is blocked, any “overkill” damage it deals will be received by the defending player. Without such an ability your mighty 9/9 creature can easily be blocked by sacrificing a cheap 1/1 (or similar), and will be much less useful.

What our model neglects here are shifts in usefulness of certain abilities like this, that make the value of the card depend from its features in a nonlinear way.

Merfolk of the Depths

To be honest, I’m convinced this card is just too damn expensive for what it does. We can still learn something from this though: There is sometimes considerable “noise” in the mana costs of cards, that is cards may have cost-usefulness ratios that differ vastly for no measurable reason. Some cards are simply bad. There is no way to predict that, you can even actually find examples of two (or more) cards that do exactly the same thing, with one just being more expensive than the other. Unfortunately that means our predictions can never be perfect.

Ornithopter, Phyrexian Walker

Both these cards have a CMC of 0, a power of 0 and our model is wrong by more than 2 CMC points. I found some other cases with power 0 wrongly predicted as well as some otehr cards with CMC 0 with wrong predictions (eg. Phyrexian Walker).

This can mean a number of things:

• Part of this can be attributed to noise (eg. the 0-mana-cost cards just happen to be better in terms of cost/utility ratio than average)
• A linear model is not sufficient for modelling Power/Toughness, at very least not when Power is 0. That is the “(Power, Toughness) to utility” relationship is not approximately linear.
• CMC behaves nonlinear even outside of the multicolor case. That is, the “utility to mana cost” relationship is not approximately linear.

Conclusions on linearity

We did get somewhat of an answer to our question (the cost of “flying” is approximately 0.79), but at the same time discovered a bunch of learning about our modelling:

• The “flying cost” question inherently assumed a linear relationship.
• However a closer look unveils that there are some nasty nonlinearities surrounding power, toughness, complex interactions of abilities.
• Moreover there is noise in the card design which makes it impossible to pin down costs for abilities exactly.
• We found that there is a latent variable which we called “utility” which can cause different mana cost configurations.

Putting all this together, our linear model is a good start. If we really want precise answers we would need to build a more complex model that allows for some non-linearities and can learn to treat different cost configurations as expressing the same utility. Or to put the other way around that can generate multiple cost configurations given a single utility value.

I think this is feasible albeit somewhat tedious, given that we can not just ramp up a network with X hidden layers to do some prediction (remember, we actually need to be able to understand the trained model in order to learn how the cost structure of MTG works!). I might go about to try this at some point in a later post, but for now I leave this as an exercise to the reader 😉

P.S.: Random idea: Could we include community ratings from gatherer.wizards.com as a means to reduce noise?

Wizards of the Coast, Magic: The Gathering, and their logos are trademarks of Wizards of the Coast LLC in the United States and other countries. © 2009 Wizards. All Rights Reserved. This web site is not affiliated with, endorsed, sponsored, or specifically approved by Wizards of the Coast LLC.