A topic thats using up my (rare) private coding time lately is the topic of how to define where an actor is allowed to walk and how it will find its way there. I found this question quite fun to work on, as it poses an interesting mix of theoretical (geometry) and practical (coding) considerations.
So what is the problem exactly? The answer is: A combination of things:
- Restrict the actors movement to a certain area that will be defined by the game programmer, I call this the walkable area.
- Come up with a mechanism that allows the actor to walk from one point in the walkable area to another one. Thereby the actor should stay in the walkable area at all times, so a path inside the area has to be found.
- When the user requests to walk to a point outside the walkable area, the actor should instead walk to some near point inside the walkable area, whereas near is not exactly defined.
It turned out I had to go through a number of idea-implementation iterations before coming up with something that works really well. Let me give you a short intro on what we did with respect to the first two points:
Discarded approaches (& why)
Pixels
A pretty intuitive idea to describe areas in a 2D game is always by just noting the pixels which belong to the area and those who don’t (for example you could save them as a black/white image). This approach has the nice practical advantage that its awesomely easy to find out for any given point whether or not it is in the walkable area. There is of course no principal necessity of those pixels to be the same size as the actual displayed pixels.
But how large should those pixels be? If we choose the pixel size too big, the walkable area will have stair-shaped edges and, even worse, walking along these blocks will look awkward as the actor will seemingly walk a zig-zag style when being requested to walk angular lines. If we choose smaller pixels however, path finding inside the walkable area will be drastically more expensive (even though, techniques like A* are applicable).
So even though there might be a sweet-spot for some situations it always feels a little dodgy working with these virtual pixels.
Walls
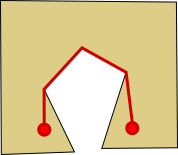
The next idea that came to mind was: Just define a number of walls (in forms of lines) the actor is not allowed to cross. If we just ensure the walls define a closed shape (e.g. by obtaining them from the edges of a polygon), there should be no chance of escape for the actor. Indeed, that is the case, at least if you have a keen eye on the corner cases of line intersection calculations.
However, path finding inside the walkable area again is a little more problematic. Take for example the picture to the left: The shortest path inside the walkable area that connects the two given points (red) goes directly along some of the edges of the polygon. That implies, that if we send the actor along that path it will walk directly along some of the walls. In the case shown here, where the target point is well inside the polygon that isn’t a big problem: We can just “turn off” the wall-crossing detection for as long as the actor walks its path and turn it back on afterwards.
The problem occurs however when the target point lies on an edge or a corner of our polygon or the walk is interrupted halfway through because the user meanwhile chose a different target: In that case the actor will stop on a point directly on a wall and it will depend on rounding whether the character is considered to be inside or outside the walkable area. Worse, if the walkable area contains a hole (like P2 or P3 in the figures below), we might end up in a situation where we don’t even know which of the two adjacent polygons (the hole and the surrounding polygon) is the walkable area the actor should return to.
Concluding, two things are missing in this approach:
- A way to identify which polygons actually belong to the walkable area and which not to avoid getting trapped outside of the walkable area if we leave it for some reason
- For positions near the border of the walkable area we also need a mechanism that can bring back the actor to a point that is guaranteed to be inside the WA.
The working approach
Components
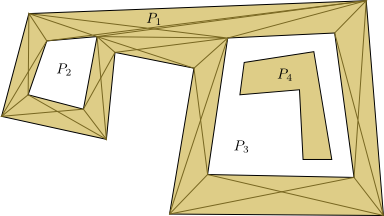

In order to tackle the first problem, we define the walkable area by a set of nested polygons. As those polygons are never overlapping we can represent them by a tree in which polygon A is a child of polygon B if it is contained in B completely. See for example the walkable area figure and the according tree. This way, we can easily check whether or not any polygon is to be considered walkable area: The outermost polygon (= root of the tree) is assumed to be walkable, everything outside of that of course is assumed not to be walkable.
Any nested polygons inside the outermost polygon are considered holes, i.e. not walkable (see P2 and P3). Polygons inside holes are again walkable areas, and so on. In the tree view that means: If the root is considered to be at level 0, all polygons on even levels are walkable and all uneven are not.
Where am I?
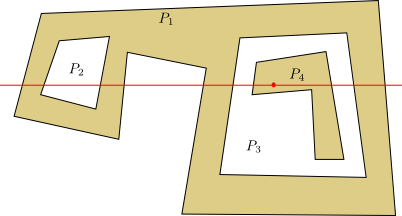
For actually finding a path given this tree of polygons, we first have to find out, in which polygon of the tree we actually are. Assume, the actor is located at the red dot in the figure. We lay a horizontal line through that position and count the number of intersections with all polygons. If the line intersects a polygon an uneven number of times on both sides, we can be sure that the point is located in the interior of that polygon. However, as there are holes, it might also be in a nested polygon. Given our polygon tree we thus conduct a binary search for the innermost polygon that contains the given point (see figure, here P4).
Having found the polygon we are navigating in, we create a map (as shown in the figure in Components for P1), that connects all area corners that can reach each other. We also connect the start and target positions accordingly (not shown in the picture). Based on that map we can conduct a Dijkstra search for the shortest path.
Theoretically it might be possible to use A* or similar approaches here to speed up the search for a lot of nodes, however I doubt any game will ever construct maps complex enough that Dijkstra will be considered too slow (if it is at one point, we can still easily replace Dijkstra with A*).
Don’t you escape!

That still leaves one problem open: What do we do when the actor is located slightly outside of a walkable polygon (e.g. in P3)? (See above for when&why this might happen). As we know we are only slightly off and we assume to work with discrete (possibly more fine granular than screen resolution) positions, we can basically just check all of the near positions until we found one that is located inside the walkable area and gently shift the actor there.
We do this by simply checking the positions on a spiral around the actors current position until we found a position that is located inside a walkable area. To avoid a very long or even endless search in case the application programmer deliberately put us into non-walkable area, we limit our efforts to a certain amount of points that are to be tested.
A possible optimization (that is not yet implemented but should be a total no-brainer), is to not check every virtual pixel, but make larger steps (e.g. 10 virtual pixels) on the spiral to save computing time (on my machine the delay for this mechanism is not noticeable even with a pixel-wise spiral though).