
In the previous post on the topic we looked into how to combine ingredients such that they fulfill various (linear) nutritional (lower- and upper-) bounds while optimizing some (linear) objective function such as total cost of the ingredients. We have seen that Linear Programs are a great way to describe these sorts of problems and shown how to use a solver library for rust to practically do it for a toy problem.
While it can be argued this is already on the mathematically more sophisticated side of dog food preparation, we’ll push it a tiny bit farther. In this post we’ll challenge a bit our modelling (in particular the objective function) and look into solver libraries for rust that allow for more general problem formulations.
What is optimal?
So far we assume the objective is to minimize (or perhaps even maximize) some property of the ingredients we select, such as total cost. At the same time we assumed that when the optimal diet required us to gauge 47.523g we would in practice be able to do this with “sufficient” precision as to not mess up the nutrient constraints.
Together these lead to a slightly weird situation: Let’s say wlog that our objective minimizes, then our optimal solution will be in some intersection of lower bounds for nutrients. Now if while measuring our dog food, we are a bit too generous, that’s likely fine (to a point), but any gram too little would violate our nutrient constraints.
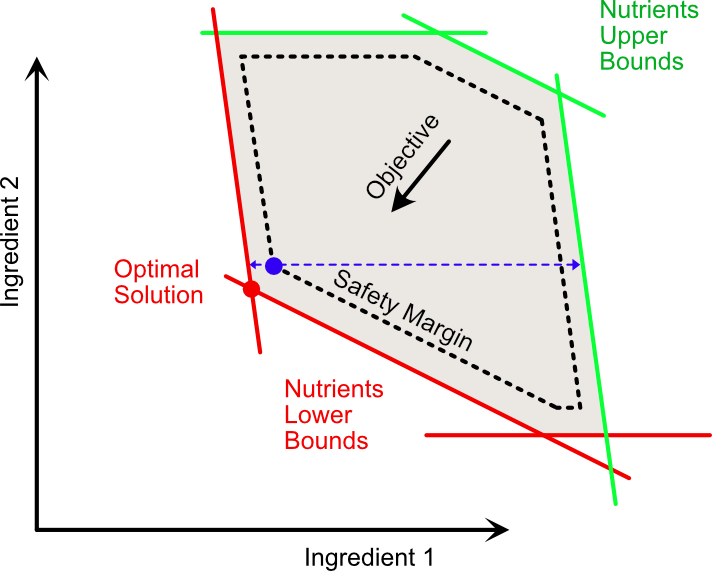
Figure 2 shows a possible way out: We can tighten the constraints a bit to create a “safety margin” (dashed) around our constraints which would give us some leeway while measuring bonemeal with the kitchen scale. Depending on where you get your nutrient bounds from, this has perhaps been already done for you to some degree (in which case you likely don’t know the actual, hard constraints).
Since some ingredients (such as meat) come in larger quantities and others (such as supplements) come in much lower, the margin “width” would ideally take that into account. Also some nutrients have a wider area compared to their masses as its very hard (but not impossible) to overdose on say some vitamins, while it may be very easy for others (not in the figure). So the “opposing” bound would also need to be taken into account as to not render the problem infeasible while leaving no space for a solution.
However some questions remain: How big is this resulting leeway for any given Ingredient in each direction (overdose/underdose)? In the figure see for example the blue point that represents the “safe” optimal solution and the blue line showing the leeway for Ingredient 1. With the known bounds and some math this can certainly be computed.
But what if what we want is actually not so much to optimize some cost, but rather want the maximum ease during meal preparation? Is there a way to move this blue dot to the “center” such that the leeway in both directions is maximal for each ingredient?
A Box of Ingredients
Consider Figure 3: For maximal measuring leeway, we would instead like to inscribe into our or feasible region a box (more specifically, rectangle in 2d-case, cuboid in 3d and so on). To ensure this box is as large as possible, we’ll want to maximize its area (volume). You could perhaps prefer other criteria here such as maximizing the leeway for the smallest-leeway-ingredient or something along those lines and use that interchangeably.
| \(l_i\) | Lower Box side for Ingredient \(i\) |
| \(u_i\) | Upper Box side for Ingredient \(i\) |
| \(A_{ij}\) | Amount of Nutrient \(j\) in Ingredient \(i\) |
| \(a_j\) | Lower bound for Nutrient \(j\) |
| \(b_j\) | Upper bound for Nutrinet \(j\) |
Tab. 1: Notation
Eqn. 1: Problem formulation.
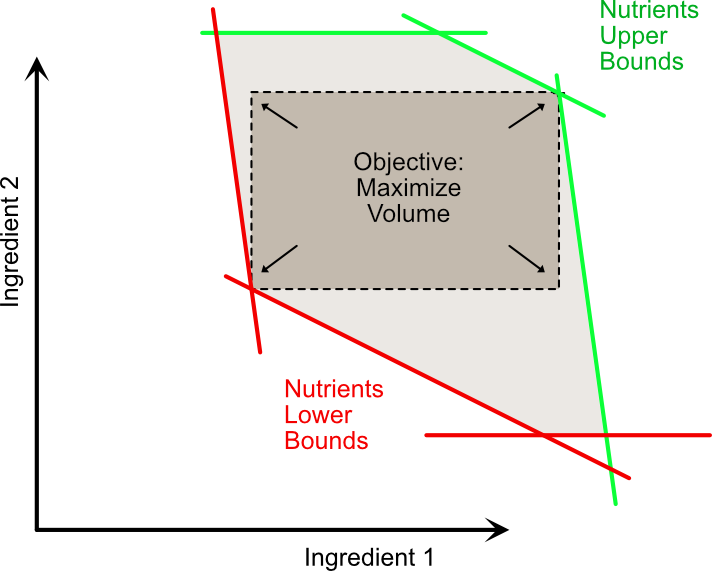
Fig. 3: Maximum “leeway box” inside the feasible region polytope.
This formulation, loosly inspired by (a brief paragraph in) [B19] should be easy enough to understand: We \(\max\)imize the product of all the edge lengths (upper box side minus lower box side), i.e. the volume. Constraints are that the lower (ingredient box) edges shan’t violate the lower (nutrient) bounds and the analogue for the upper edges. And of course upper edges should be higher values than lower edges and there should still be no negative ingredients amounts.
Some Options for Rust Solvers
There isa couple of libraries out there for Rust that give you access to linear and non-linear solvers of various sorts. The table below shows a comparison which is by no means fair or complete (eg. argmin contains a lot of algorithms while others on this list contain very few or only one).
In our case, we (still) have linear constraints (our nutrient bounds), but our objective function is non-linear. Since it is however quadratic, it qualifies as convex and could for example be solved neatly with totsu. In our example we opted instead for cobyla which is slightly more general and thus allows us to experiment with our target function more freely.
| Variable Constr. | Linear Constr. | Convex Constr. | Arbitrary Constr. | Linear Objective | Convex Objective | Arbitrary Objective | Derivative-Free | |
|---|---|---|---|---|---|---|---|---|
| good_lp | ✓ | ✓ | ✓ | – | ||||
| totsu | ✓ | ✓ | ✓ | ✓ | ✓ | – | ||
| argmin | ✓ | ✓ | ✓ | (✓) | ||||
| gomez | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| ipopt-rs | ✓ | ✓ | ✓ | ✓ (2x diffable) | ✓ | ✓ | ✓ (2x diffable) | |
| cobyla | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Rust Implementation
Again, the full source code is available on Github, here is the relevant solving function for Cobyla:
use cobyla::{fmin_cobyla, CstrFn};
use crate::diet_problem::DietProblem;
// Our variables are one flat vector of values,
// we interleave lower and upper rectangle sides for each of the dimensions,
// these compute the indices into the variable vector.
pub fn lower(i: usize) -> usize { i * 2 }
pub fn upper(i: usize) -> usize { i * 2 + 1 }
pub fn optimize_cobyla(problem: &DietProblem) {
// Cobyla constraints are CstrFn (constraint functions) defined
// as Fn(&[f64]) -> f64, in our case, closures (which each have their own unique concrete type, hence the dyn).
// In order to make these closures live longer than the scope they were defined in (which is
// the loop body), we need to put them in a box.
let mut boxed_constraints = Vec::<Box::<dyn CstrFn>>::new();
// Create a constraint for each lower nutrient bound
for (nutrient, minimum) in &problem.minima.nutrients {
// Make a closure that computes by how much we violate this bound
// and put it into the box. Move in the ref to `problem`.
let constraint = Box::new(move |x: &[f64]| {
// Sum up over all ingredients i
// The amount of nutrient `nutrient` in that ingredient times the lower rectangle
// side of ingredient i
let s: f64 = problem.ingredients
.iter()
.enumerate()
.map(|(i, ingr)| { ingr.nutrients.get(&nutrient.clone()).unwrap_or(&0.0) * x[lower(i)] })
.sum();
// ... and demand it is >= the minimum
f64::min(minimum.clone() - s, 0.0)
});
boxed_constraints.push(constraint);
}
// Analog for upper bounds
for (nutrient, maximum) in &problem.maxima.nutrients {
let constraint = Box::new(move |x: &[f64]| {
let s: f64 = problem.ingredients
.iter()
.enumerate()
.map(|(i, ingr)| { ingr.nutrients.get(&nutrient).unwrap_or(&0.0) * x[upper(i)] })
.sum();
f64::min(s - maximum, 0.0)
});
boxed_constraints.push(constraint);
}
// Cobyla expects a Vec<&dyn CstrFn> which we can now obtain by "unboxing" the
// `boxed_constraints`.
// &** is because "reference to box of CstrFn" -> "reference to CstrFn"
let constraints: Vec<&dyn CstrFn> = boxed_constraints.iter().map(|b| &**b).collect();
fn cost(x: &[f64], _data: &mut ()) -> f64 {
// Compute volume
let mut volume = 1.0;
for i in 0..(x.len() / 2) {
// x has, for each ingredient, a lower bound and an upper bound
// volume is the product of all of those that are actually included
if x[lower(i)] != 0.0 && x[upper(i)] != 0.0 {
volume *= x[upper(i)] - x[lower(i)];
}
}
volume
}
// For each dimension/ingredient we have a left- and right box side
let mut x = vec![0.0; problem.ingredients.len() * 2];
// Actually run cobyla with some parameters
let (status, x_opt) = fmin_cobyla(cost, &mut x, &constraints, (), 0.5, 1e-4, 2000, 1);
println!("COBYLA status {:?} x_opt {:?}", status, x_opt);
for (i, ingredient) in problem.ingredients.iter().enumerate() {
println!("{:20}: {:5.2} .. {:5.2}", ingredient.name, x[lower(i)], x[upper(i)]);
}
}
Bibliography
[B19] Mehdi Behroozi. Largest Inscribed Rectangles in Geometric Convex Sets. 2019. https://arxiv.org/abs/1905.13246.
Hi, thanks for sharing this example. I think the link to the source in github.com is broken.
Thanks for the hint, should be fixed now!