
Optimize your own Dog Food
In this post we’ll look into how to make your own dog food, seen as an optimization problem. I’ll give a short background intro into this way of feeding your dog (called BARF), which I’m by no means an expert in. What you thus can not expect from this article is specific guidance on what the best nutrition for your dog is.
But maybe I can make you a bit curious about linear optimization.
BARF
There are various ways to feed your dog, from dried and canned food of various sorts and qualities over half-prepared meals and cooking yourself to BARF.
BARF originally refers to “Bone and Raw Food” but nowadays is usually retrofitted as meaning “Biologically Appropriate Raw Food”. As both names imply, the diet revolves around raw ingredients. While ready-to-thaw BARF mixes exist, a lot of people mix fresh ingredients for individual meals of their pets.
Reasons for a BARF diet are plentiful and so are reasons to avoid it. A full discussion would derail the scope of this article, but if you are interested to know more, I can only urge you to weigh all the pros and cons and listen to the vet of your trust perhaps a little more than the friendly BARF store owner. A really complete and differentiated view of the topic can be found in the works of Julia Fritz [F18] (German). Most importantly, do not take nutrient limits lightly. It turns out, compared to the amount of food they eat, dogs need much more nutrients than humans or wolves.
We will consider the case of preparing a meal for your dog (or any other animal, really) with certain nutrient constraints from a, lets say, somewhat theoretical standpoint.
An Optimizers Perspective
At our disposal are a certain number of Ingredients such as Beef, Apples, Bone, whatever have you. Each ingredient has a specific (linear) cost attached to it, which may be its price per kilogram or simply 0 in case we don’t care. An ingredient (obviously) cant be negative, having -20g of something in a meal simply does not make sense.
Each such ingredient holds some amount of Nutrients such as Fat, Protein or Vitamin A. For our purposes we can also treat properties like energy content and mass as nutrients, as they behave the same in our calculations. Nutrients scale linearly with its mass. I.e. if 100g of Fumblesauce contains 20g of Fat, then we assume 1kg will contain 200g and so forth. We also assume we can meter our ingredients to sufficient precision so that obtaining 123.4567g of Gobblermeat or something “close enough” is possible (we might get back to this in a future post).
Note that units don’t matter so much here but are just for illustration. As long as we keep it consistent, we can even have different units for measuring the amount of each nutrient; but of course in all contexts in which we use that nutrient, we have use the same scale. To make this article simpler we’ll completely ignore units here, but when you actually work with the data you may want to spend a minute or two to think about them.
Our goal is, of course to obtain a meal (that is a combination of ingredients of some amounts), that fulfills a certain minimum and maximum amounts for certain ingredients. Some of these may have only a lower OR upper bound (i.e. it may not matter if you have too much of some specific Vitamin), some may be bounded from above and below.
Table 1 shows some notation for Variables. Equipped with these, we can formulate or problem as a Linear Program (right next to the table). Note the term “program” may be a bit misleading here (but that’s what its called). It is nothing more than an optimization criterion (minimize the price) and some inequality constraints.
| \(x_i\) | How much of ingredient \(x\) to take (what we want to find out) |
| \(A_{ij}\) | Amount of nutrient \(j\) contained in ingredient \(i\) |
| \(a_j\) | Minimum amount of nutrient \(j\) (lower bound) |
| \(b_j\) | Maximum amount of nutrient \(j\) (upper bound) |
| \(c_i\) | Cost of ingredient \(i\). \(c^T x\) is called the Objective Function. |
Tab. 1: Notation for the Dog Diet Problem
Eqn. 1: Linear Program for the Dog Diet Problem.
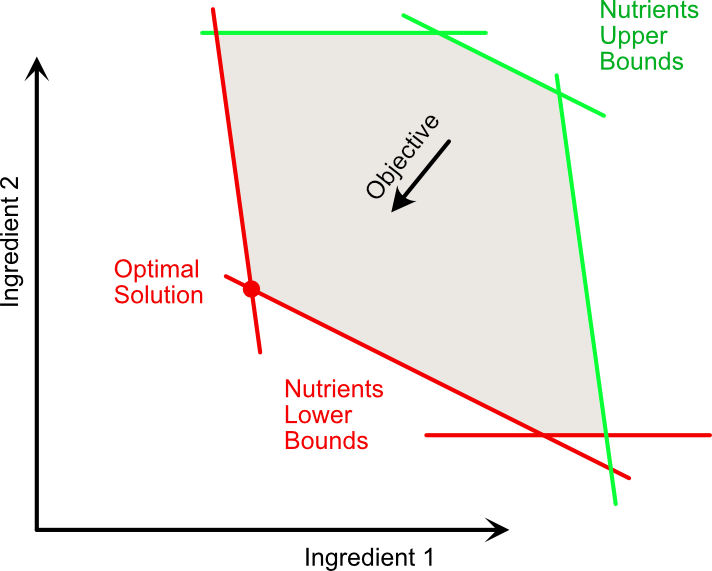
Fig. 2: Illustration of the Dog Diet Problem for 2 ingredients.
Linear Programs are nice, because they can in practice be solved efficiently and many highly optimized solvers are available. There is enough to be said about linear programs to fill a entire books about them (and people have, there is a lot of content to find), but for our purpose it will be enough to know there are black boxes out there for most programming languages / computation environments that solve these kinds of problems very efficiently.
It reads like this: We want to minimize the product of the cost vector \(c\) (eg monetary cost of the ingredients) and our variable ingredient amount vector \(x\) subject to having the product of the ingredient-to-nutrients-amount-matrix \(A\) and the ingredient amount \(x\) (that is the total number of nutrients in the end) be constrained to be between \(a\) and \(b\). Also, there shant be negative amounts of ingredients so \(x \ge 0\). As a side note, there is always an optimal solution in some “corner” (intersection of constraints), Figure 2 might provide some visual intuition to convince you (actual proofs for this exist of course).
Rust implementation
First, we create a couple of structs to hold our data:
#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]
pub enum Nutrient {
Energy,
Protein,
Calcium,
// ...
}
// ...
#[derive(Default)]
pub struct Ingredient {
pub name: String,
pub nutrients: HashMap<Nutrient, f64>,
}
// ...
pub struct DietProblem {
pub minima: Ingredient,
pub maxima: Ingredient,
pub ingredients: Vec<Ingredient>,
}
So a Nutrient for us is an enum that tells us which nutrient we are talking about, an Ingredient in contrast has an actual name and a number of nutrients with amounts. The problem we want to solve is a DietProblem which has some lower and upper bounds of nutrients (expressed as Ingredients) and a vector of ingredients to choose from.
I also could not resist to add a little macro to allow to define them conveniently:
let minima = ingredient!{ (min) Energy: 1000.0, Protein: 100.0, Calcium: 1.0 };
let maxima = ingredient!{ (max) Energy: 1100.0, Protein: 200.0, Calcium: 2.0 };
let mut d = DietProblem::new(minima, maxima);
d.add(ingredient!{ (GobblerMeat) Energy: 1.25, Protein: 0.28 });
d.add(ingredient!{ (BulbFruit) Energy: 1.0 });
d.add(ingredient!{ (FrobnizerBone) Energy: 1.0, Calcium: 0.01 });
Admittedly, that might be a bit on the questionable side but it is readable and super fun to write.
For the actual solving the use the Rust crate good_lp which wraps a couple of LP solvers and has a pretty nice API:
pub fn optimize_good_lp(problem: &DietProblem) {
// Good LP variables. These are the values we want to optimize,
// in our case amounts of ingredients.
let mut variables = variables!();
let mut amounts = HashMap::<String, Variable>::new();
// Good LP expressions that express how much of each nutrient
// our solutions will have.
let mut nutrient_sums = HashMap::<Nutrient, Expression>::new();
for ingredient in problem.ingredients.iter() {
// Create variable tracking how much of this ingredient we'll use
let amount = variables.add(variable().min(0));
amounts.insert(ingredient.name.clone(), amount);
// Extend nutrient expressions
for (nutrient, contents) in ingredient.nutrients.iter() {
*nutrient_sums.entry(*nutrient).or_default() += amount * *contents;
}
}
// Here: Maximize "0" (i.e. just find any solution that obeys the constraints).
// This could instead be minimizing the cost of the ingredients or
// something along those lines
let mut lp = variables.maximise(0).using(default_solver);
// Add constraints: We want at least all the nutrients in
// the `problem.minima` "ingredient"
// and most those in `problem.maxima`.
for (nutrient, contents) in problem.minima.nutrients.iter() {
lp.add_constraint(
constraint!(nutrient_sums[&nutrient].clone() >= *contents)
);
}
for (nutrient, contents) in problem.maxima.nutrients.iter() {
lp.add_constraint(
constraint!(nutrient_sums[&nutrient].clone() <= *contents)
);
}
// Actual work happens here:
let solution = lp.solve().unwrap();
}The full source code can be found in https://github.com/Droggelbecher/dogfood, enjoy!
Bibliography
[F18] Julia Fritz. Hunde barfen. 2018. 2. Auflage. ISBN 978-3-8001-0924-1, Ulmer-Eugen Verlag.
1 thought on “Optimize your own Dog Food”