In the previous posts in this series we dug into some data analysis on Magic the Gathering cards and tried to model the mana cost of cards in order to answer questions like “how much does ‘flying’ cost?”.
We found a linear model that could explain the costs to some degree, however it struggled to get right the more complex cost structure around eg. 0-mana or many-colered cards. In this post we make an attempt at a neural network model of MTG mana costs in order to address these nonlinearities.
In the previous post, I made a point out of wanting a model that is interpretable. Even though the relationship does not seem to be linear, there could be some approaches to make this happen such as including quadratic terms in the linear regression, or try to build a more informed/complex model that would try to capture our mental intuition on the mana price structure (and still makes sense to a human).
As it is somewhat easier and I had the emotional urge to want to try it, this post will not do any of those but try to learn a tensorflow model.
As we learned in the last post, the same card could have a cost of “one mana of each of the five colors” or lets say “2 green plus 5 of any color” and they would be in the same ballpark of “cheapness” (if this doesn’t make sense to you, take another look at that article). That is, if we are to make a model that from a description of the card would try to predict its mana cost directly it would have to make multiple predictions for different color combinations or, alternatively get the desired color combination as an additional input.
Modelling
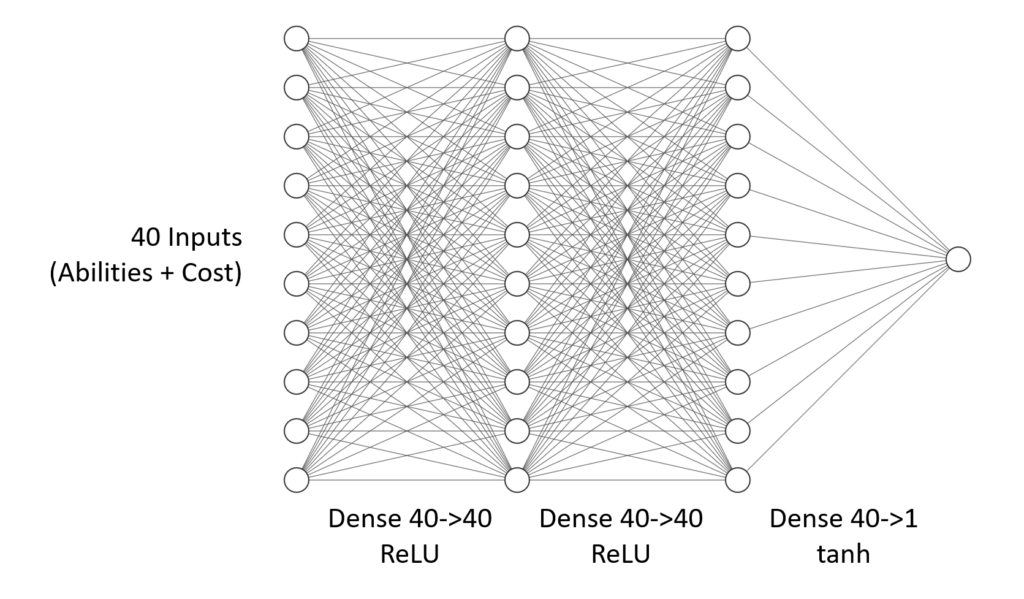
As we want to keep it simple, instead we will predict in a slightly different way: The model input will be a description of the card including the mana cost and the output will be a number in the range -1 (“too cheap”) to +1 (“too expensive”).
We build a simple dense network like so:
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(40,)),
tf.keras.layers.Dense(40, activation=tf.nn.relu),
tf.keras.layers.Dense(40, activation=tf.nn.relu),
tf.keras.layers.Dense(1, activation=tf.nn.tanh)
])
model.compile(optimizer='adam',
loss='mse',
metrics=['mse', 'mean_absolute_error'])
Evaluation
The mean squared error of the test set is 0.0827. Lets look at some concrete test set predictions (ordered by loss):
| Name | loss | Prediction | Ground Truth |
|---|---|---|---|
| Knight of Meadowgrain-white | 0.00 | -1.00 | -1 |
| Feral Abomination-black | 0.00 | -1.00 | -1 |
| Bitterbow Sharpshooters-green | 0.00 | -1.00 | -1 |
| Risen Sanctuary-green | 0.00 | -1.00 | -1 |
| Ambush Viper-green | 0.00 | -1.00 | -1 |
| … | |||
| Raging Bull | 0.01 | 0.08 | 0 |
| Risen Sanctuary+green | 0.01 | 0.92 | 1 |
| Alaborn Grenadier | 0.01 | 0.09 | 0 |
| Coral Eel | 0.01 | 0.10 | 0 |
| … | |||
| Golgari Longlegs-green | 0.23 | -0.52 | -1 |
| Hobgoblin Dragoon | 0.29 | 0.54 | 0 |
| Minotaur Aggressor-red | 0.41 | -0.36 | -1 |
| Goblin Champion | 0.41 | 0.64 | 0 |
| Feral Abomination | 0.56 | -0.75 | 0 |
| Phyrexian Walker | 0.88 | -0.94 | 0 |
| Ornithopter | 0.96 | -0.98 | 0 |
As before, lets take a look at a few of the worst predicted cards:

Pred.: -0.98 (cheap) GT: 0

Pred.: -0.94 (cheap) GT: 0

Pred.: -0.75 (cheap) GT: 0
Ornithopter, again! As with our linear model, this one seems incredible hard to predict. Indeed if we take a look at all the creatures with cost 0, both Ornithopter and Phyrexian Walker are rather good value for the money, so we can not really blame our model (note “Shield Sphere” was not considered as it has more complex ruling text). Similarly, with Feral Abomination, there are few examples for “big” deathtouch creatures.
Sorry for the weird query string in this URL, it was the easiest method I could find to exclude the many cards with complex rulings that were not considered.
It so happens that out of these four the only comparable card (Vampire Champion) is also in the test set, so the data sparsity problem strikes again. If we go farther up the list we already see the loss decreasing pretty quickly (Goblin Champion is already at 0.41), and since we did not spent a lot of time yet fine-tuning the model, there is probably a lot of potential to reduce these further.
Just out of curiosity, lets look what our model made out of some of the problem cases from last post. All these are taking with a grain of salt though as these ended up in the training set.
That is, the model could have memorized / overfit on these specific cards. The reason for the new train/test split is new magic cards came out in the mean while and the mtg-json API changed, so even with a fixed random seed I got a different train/test split.
| Name | loss | Prediction | Ground Truth |
|---|---|---|---|
| Merfolk of the Depths-green | 0.12 | -0.65 | -1 (*) |
| Merfolk of the Depths+white | 0.00 | 1.00 | +1 |
| Merfolk of the Depths | 0.00 | -0.02 | 0 |
| Wall of Torches-red | 0.00 | -0.96 | -1 |
| Wall of Torches | 0.01 | 0.08 | +0 |
| Wall of Torches+red | 0.00 | 0.99 | 1 |
| Hussar Patrol+green | 0.00 | 0.99 | +1 |
| Hussar Patrol-blue | 0.00 | -0.95 | -1 |
| Hussar Patrol | 0.01 | -0.08 | 0 |
| Fusion Elemental-green | 0.00 | -0.99 | -1 |
| Fusion Elemental+white | 0.00 | 0.98 | +1 |
| Fusion Elemental | 0.01 | 0.07 | 0 |
| Kalonian Behemoth-green | 0.00 | -1.00 | -1 |
| Kalonian Behemoth+blue | 0.00 | 0.96 | +1 |
| Kalonian Behemoth | 0.13 | 0.36 | 0 |
*) I must admit this one might be a bit nonsensical. We’re encoding the split-mana cost like “green OR blue” as if it would cost both eg “green AND blue”, while the model still gets passed a CMC that counts these splits as just one. By just randomly removing the green part of a split mana cost encoded this way, we provide the model an opportunity to cheat. Overall I think this encoding is less than ideal, there are probably better ways to do it.
Using the Oracle
Now we have a model that can tell us whether a card is too expensive or too cheap, but how does that help us with the original question of determining the cost of flying? Well, in this case there is a surprisingly simple answer: Since the model is rather simple, the forward-evaluation is fast so we can just evaluate all configurations we are interested in with and without flying to see how that changes the flying cost.
That’s exactly what you see below, we pick a certain simple creature template (common colorless creature printed around April 2019). Then we first consider the non-flying case in which we vary power and toughness and for each such combination find the mana cost for which our model outputs the value closest to 0 (i.e. the approximately correct mana cost according to the model). Thats the value you see in the table cells below, followed by the model output in parenthesis. We then repeat the same for flying (unsurprisingly, the costs are somewhat higher). By subtracting the two tables from each other we can now obtain a picture of the cost of flying depending on power and toughness for our queried scenario:
Cost without flying
| Pwr/Tough | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 0 (+.21) | 1 (+.06) | 2 (-.02) | 3 (-.03) |
| 1 | 2 (+.04) | 2 (+.05) | 3 (-.02) | 4 (-.03) |
| 2 | 3 (+.01) | 3 (+.04) | 4 (+.01) | 5 (-.02) |
| 3 | 3 (-.01) | 4 (+.07) | 5 (+.06) | 6 (+.02) |
| 4 | 4 (+.09) | 4 (-.01) | 5 (+.08) | 6 (+.02) |
Cost with flying
| Pwr/Tough | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 1 (+.28) | 1 (+.11) | 2 (+.15) | 3 (+.16) |
| 1 | 3 (+.13) | 3 (+.11) | 3 (+.05) | 4 (+.10) |
| 2 | 5 (+.04) | 4 (-.04) | 5 (+.08) | 5 (+.03) |
| 3 | 5 (+.01) | 5 (-.01) | 6 (+.09) | 6 (+.06) |
| 4 | 6 (+.09) | 6 (+.07) | 7 (+.11) | 7 (+.09) |
Difference
| Pwr/Tough | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 2 | 1 | 1 | 0 |
| 3 | 2 | 1 | 1 | 0 |
| 4 | 2 | 2 | 2 | 1 |
For interpretation of this alas, we have to be a bit careful still: According to this, e.g. a hypothetical “common” colorless 3/6 creature is worth 6 mana no matter whether it has flying or not, which does not seem right. Again, this issue is likely due to sparsity combined with card cheapness “noise”, as only few examples in that area exist [1] in our limited dataset of simple creatures. On the upside, we do get at least a vague idea of the nonlinear flying cost: It seems to be becoming more valuable with stronger creatures (which makes sense if you ever played the game).
Wizards of the Coast, Magic: The Gathering, and their logos are trademarks of Wizards of the Coast LLC in the United States and other countries. © 2009 Wizards. All Rights Reserved. This web site is not affiliated with, endorsed, sponsored, or specifically approved by Wizards of the Coast LLC.